Pullonkaula, vaihtelu ja parannus
Jatketaan prosessimme tutkimista ja otetaan askel kohti reaalimaailmaa, vaihtelu astuu kuvaan mukaan. Mitä se tarkoittaa ja miten reagoimme tilanteeseen?
Tämä artikkeli on jatkoa aikaisemmin kirjoittamilleni artikkeleille ja suosittelen tutustumista myös niihin, jotta tiedätte, miten tähän tilanteeseen on päästy.
Artikkeli: Pullonkaulat ja parantaminen (17.11.2021)
Artikkeli: Pullonkaulan löytäminen (4.12.2021)
Artikkeli: Pullonkaulan hyödyntäminen (8.12.2021)
Tähän mennessä olimme siis prosessia mittaamalla ja tuloksia analysoimalla selvittäneet prosessin pullonkaulan, päättäneet miten hyödynnämme pullonkaulaa ja alistaneet muun toiminnan tälle päätökselle. Ideaalimaailmassamme prosessimme pystyy vastaamaan asiakaskysyntään (80 kpl/d = 0,19 kpl/min). Kuitenkin kun mittaamme prosessiamme, saamme keskimääräiseksi ulostuloksi ainoastaan 72 kpl/d (0,16 kpl/min), samalla kun keskeneräisen työn määrä prosessissa on keskimäärin 35 kpl. Samaan aikaan mittaukset osoittavat, että prosessin jaksoaika, eli aika, jonka yksittäiseltä tuotteelta tai palvelulta kestää kulkea prosessin läpi on lähes neljä tuntia (222 minuuttia). Kun nämä tiedot lisätään aikaisemmassa artikkelissa nähtyihin virtauskuviin, näyttää tilanne seuraavalta:
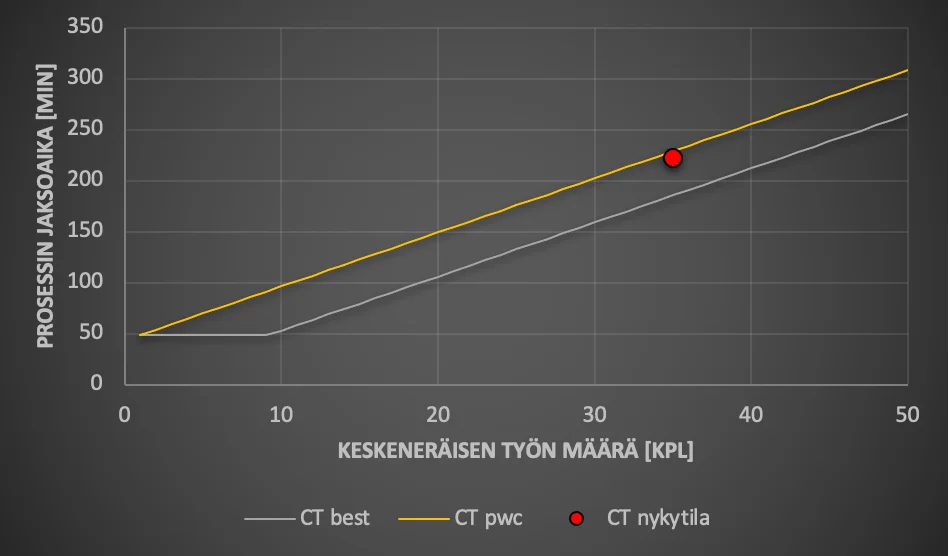
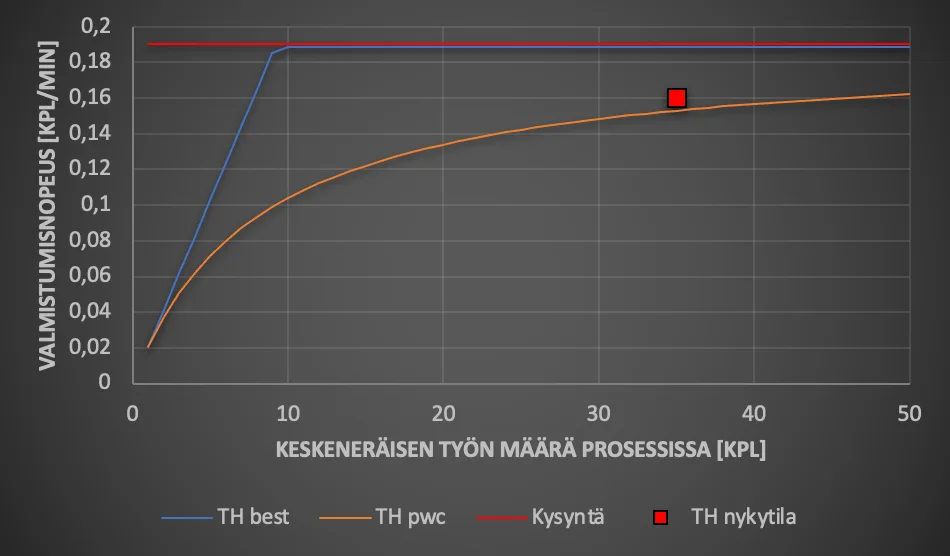
Molemmissa kuvissa parhaan tapauksen kuvaajat (CT best ja TH best) kuvaavat tilannetta, jossa vaihtelua ei ole ja juuri vaihtelu aiheuttaa sen, ettemme saavuta ideaalitilannetta. Prosessimme tilanne voisi toki olla huonompikin, todellisen tilanteen sijoittuminen parhaan tapauksen ja käytännön huonoimman tapauksen väliin tarkoittaa, että prosessimme toimii jo kohtuullisen tehokkaasti.
Kuitenkin joudumme tekemään ylitöitä täyttääksemme päivittäisen asiakastarpeen. Samalla asiakkaat ovat tyytymättömiä vasteaikaamme ja yrityksen johto asettaakin kunnianhimoiseksi tavoitteeksi jaksoajan laskemisen alle kahteen tuntiin. Miten voimme siis vastata asiakastarpeeseen normaalin työajan puitteissa (eli lisätä kapasiteettia) ja samalla lyhentää jaksoaikaa?
Jos siis haluamme lyhentää jaksoaikaa (Kuva 1), pitää keskeneräisen työn määrää vähentää. Toisaalta, jos vähennämme keskeneräisen työn määrää, valmistumisnopeutemme laskee (Kuva 2). Melkoinen ristiriita ja saattaa tulla monelle yllätyksenä.
Onneksi tiedämme missä prosessin pullonkaula sijaitsee (vaihe kuusi) ja tiedämme että kannattaa pitää silmällä myös käyttösuhteeltaan tätä lähellä olevaa vaihetta (vaihe neljä), koska siitä tulee seuraava pullonkaula, jos vaiheeseen kuusi kohdistetaan parannustoimenpiteitä.
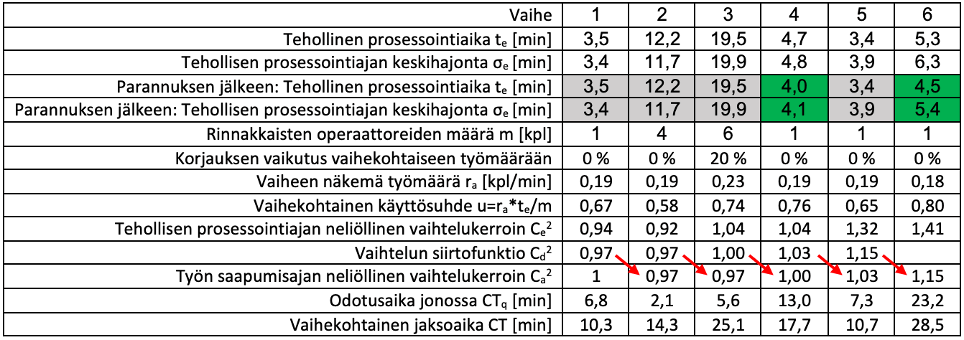
Tutkitaan seuraavaksi vaihtelun vaikutusta prosessissamme tapahtuvaan jonoutumiseen, eli miksi jaksoaika on 222 minuuttia, eikä aikaisemmassa artikkelissa laskettu raaka prosessointiaika 49 minuuttia? Prosessista mitatut teholliset prosessointiajat olivat siis useiden mittausten keskiarvoja, keskiarvojen lisäksi samoista mittaustuloksista voidaan laskea vaihekohtaiset keskihajonnat prosessointiajoille. Lisätään nämä aikaisemmassa artikkelissa esitettyyn taulukkoon.

Otetaan avuksi Kingmanin yhtälö, joka kuvaa odotusaikaa jonossa CTq.
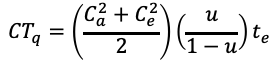
jossa
te = tehollinen prosessointiaika
u = käyttösuhde
Ca2 = työn saapumisajan neliöllinen vaihtelukerroin
Ce2 = tehollisen prosessointiajan neliöllinen vaihtelukerroin
Tilanteessa, jossa vaiheessa on rinnakkaisia operaattoreita/koneita kaavaan tulee lisää termi m (rinnakkaisten operaattoreiden määrä).

Ce2 voidaan laskea olemassa olevasta datasta kaavalla
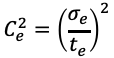
Oletetaan lisäksi työn saapumisajalle keskimääräinen vaihtelu, jolloin Ca2=1.
Kun vielä tiedetään, miten työn saapumisajan vaihtelu saadaan linkitettyä prosessin muihin vaiheisiin, voidaan aloittaa varsinainen laskenta.
Kun vaiheessa ei ole rinnakkaisia operaattoreita on vaihtelun siirtofunktio
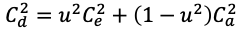
Ja rinnakkaisten operaattoreiden tapauksessa
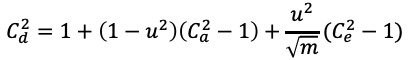
Nyt tiedämme vaiheen n+1 työn saapumisajan neliöllisen vaihtelukertoimen, joka on
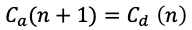
Paljon monimutkaisilta vaikuttavia kaavoja, onneksi taulukkolaskentaohjelmat hoitavat raa’an laskennan puolestamme, mutta tietynlainen ymmärrys kaavoista on hyödyllistä sisäistää. Sekä jonotusajan muodostumiseen, että vaihtelun siirtymiseen vaiheesta toiseen vaikuttaa sekä vaihtelu (C), että käyttösuhde (u). Käyttösuhteen merkitys korostuu, mitä suurempi se on. Ja suurimmillaan se on juuri prosessin pullonkaulassa, tässä yksi syy sille miksi pullonkaulan löytämiseen, hyödyntämiseen ja parantamiseen pitää panostaa.
Kun vielä tiedämme, että vaiheen jaksoaika koostuu jonotusajasta ennen vaihetta ja prosessointiajasta vaiheessa (CT = CTq + te), voimme laskea taulukkoon muutaman lisärivin.
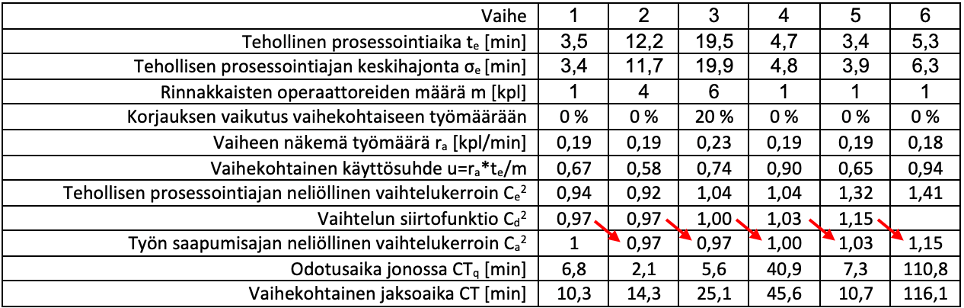
Kun laskemme vaihekohtaiset jaksoajat yhteen, saamme koko prosessin jaksoajan CTtot222 minuuttia, eli ajan, joka yksittäiseltä tuotteelta tai palvelulta kuluu prosessin läpi kulkemiseen.
Laskemalla vaihekohtaisesti suhdeluvun teholliselle prosessointiajalle ja jaksoajalle, saamme selville Lean-termein arvoa lisäävän ajan osuuden ja samalla käsityksen paljonko kussakin prosessivaiheessa on odotuksesta johtuvaa ”hukkaa”.

Miten tätä ”hukkaa” sitten lähdetään poistamaan? Ongelmaa ei voi ratkaista samalta tasolta jolta se on asetettu. Hukkaa ei voi poistaa hukkaa tutkimalla. Hukka on seuraus, syyt ovat muualla. Ja syyt on onneksi jo kerrottu aikaisemmin mainituissa tehdasfysiikan kaavoissa.
Kingmanin yhtälö voidaan kirjoittaa yksinkertaisemmin muotoon:
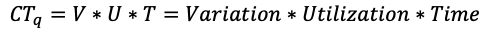
Eli jos haluamme vaikuttaa jonotusaikaan meidän on vaikutettava joko vaihteluun, käyttösuhteeseen tai aikaan. Kun samalla muistamme, että käyttösuhteen laskennassa mukana ovat saapumisnopeus, prosessointiaika ja rinnakkaisten operaattoreiden määrä (u=ra*te/m) alkaa tilanne selkeytyä.
Kohteena on siis pullonkaula (vaihe kuusi) ja sitä käyttösuhteeltaan lähinnä oleva vaihe (vaihe neljä), haluamme pitää pullonkaulan tiedossa, emme joutua tilanteeseen, jossa pullonkaula vaihtaa paikkaa parannuksen jälkeen. Vaihtoehtoja ovat vaihtelun pienentäminen, tarvittavan prosessointiajan vähentäminen ja rinnakkaisten operaattoreiden lisääminen vaiheisiin.
Rinnakkaisten operaattoreiden lisääminen tarkoittaa yleensä investoimista, investoimista työvoimaan, investoimista koneisiin, tai molempiin, joten monesti on hyödyllistä tutkia ensin muut vaihtoehdot.
Teholliseen prosessointiaikaan te sisältyy itse työvaiheen suorittamisen lisäksi myös kaikki ongelmatilanteet, keskeytykset jne. eli vähentämällä näitä pystymme vaikuttamaan tarvittavan prosessointiajan määrään. Työkaluista ei ole puutetta, esim. Lean-sateenvarjon alta löytyy useita juuri tällaiseen tarpeeseen kehitettyjä menetelmiä. Käytämme tässä esimerkissä menetelminä 5S:ää, virheenestimiä (poka-yoke) ja työn standardointia. Kaikkien näiden tarkoituksena on siis vähentää tarvittavaa prosessointiaikaa ja pienentää prosessointiajan vaihtelua. Työkalujen valinta on toki aina tapauskohtaista, mutta yllä mainitut ovat useisiin tapauksiin soveliaita valintoja.
Tehdään parannusten vaikutuksista konservatiivinen oletus, vaiheiden neljä ja kuusi tehollinen prosessointiaika ja prosessointiajan vaihtelu pienenevät kummatkin 15 %. Lasketaan mitä tämä tarkoittaa prosessimme jaksoajalle ja kapasiteetille.
Koko prosessin jaksoaika CTtot ≈107 minuuttia. Kun pienensimme prosessointiaikaa ja ajan vaihtelua 15 % kahdessa prosessivaiheessa lyheni koko prosessin jaksoaika yli 50 %! Samalla prosessimme kapasiteetti (pullonkaulan valmistumisnopeus) arvosta 0,19 kpl/min arvoon 0,22 kpl/min ( ∼100 kpl/d).
Piirretään uudesta tilanteesta virtauskuva, siten että sekä valmistumisnopeus, että jaksoaika ovat samassa kuvassa. Keskeneräisen työn määrä prosessissa on Littlen lain mukaisesti.
WIP=CT X TH, eli Keskeneräisen työn määrä = Jaksoaika X Valmistumisnopeus
WIP = 107 minuuttia x 0,22 kpl/min = 24 kpl
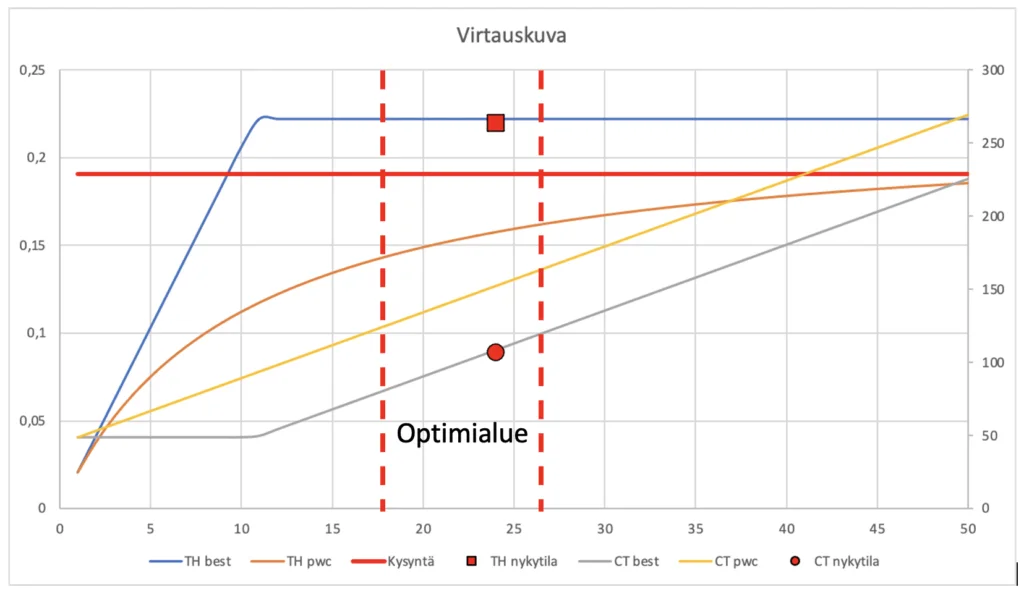
Koska pullonkaulan valmistumisnopeus lisääntyi parannuksen seurauksena, myös prosessin ns. kriittisen WIP:n taso (katso aikaisempi artikkeli) nousi hieman (W0=11 kpl). Prosessissa täytyy aina olla vähintään tämän verran keskeneräistä työtä tai ulostulonopeus romahtaa.
Kuvaan 3 on myös merkitty optimialue, jolla kannattaa pysyä, jottei toisaalta riskeerata ulostulon romahtamista ja toisaalta pidetään prosessin jaksoaika tavoitteen mukaisena. Optimialueella pysymiseksi otamme käyttöön CONWIP-menetelmän (constant work in process), eli rajoitamme keskeneräisen työn määrän prosessissa tiettyyn arvoon. Yksinkertaisimmillaan tämä tarkoittaa sitä, että jokaisen työn mukana kulkee ns. CONWIP-kortti, joita on prosessisa vain tietty määrä ja uuden työn saa vapauttaa prosessiin vain vapaata korttia vastaan. Tietenkin teknisemmätkin toteutukset ovat mahdollisia. Tässä esimerkissämme CONWIP-korttien määrä voisi olla juuri Littlen lain avulla laskettu 24 kpl.
Mitä tästä kaikesta kannattaa muistaa?
- Vaihtelu heikentää aina systeemin suorituskykyä, reaalimaailmassa, jossa vaihtelua aina esiintyy teoreettisia suorituskykymaksimeja ei saavuteta kuin korkeintaan hetkellisesti
- Systeemit suojautuvat vaihtelua vastaan, varastoilla, kapasiteetilla tai ajalla (tai jollain näiden yhdistelmällä), esimerkissämme tarvittiin lisää kapasiteettia ja jaksoaika oli pitkä
–> Vaihtelu pitää tunnistaa ja ymmärtää
- Ketju on vain niin vahva kuin sen heikoin lenkki, prosessin pullonkaula määrää sen ulostulonopeuden
- Pullonkaula pitää löytää, hyödyntää ja muiden vaiheiden pitää toimia pullonkaulalle alisteisesti.
–> Kehitystoimenpiteet pitää kohdentaa ensisijaisesti pullonkaulaan
- Prosessien toimintaa säätelevät tietyt lainalaisuudet, jotka tunnetaan tehdasfysiikkana tai operaatiotieteinä
- Nämä lainalaisuudet tuntemalla pystytään tekemään päätöksiä tieteellisin perustein, ei uskomuksien pohjalta
- Tehdasfysiikka nimen ei pidä antaa hämätä, lainalaisuudet pätevät kaikessa prosessimaisessa toiminnassa (tuotteet ja palvelut), ei pelkästään valmistavassa teollisuudessa
–> Ensisijaisesti tehdasfysiikka tarjoaa mielenmallin lainalaisuuksista, vaikkakin myös laskenta on mahdollista
Lähteet:
- Eliyahu M. Godratt, The Goal, 1984 (suomeksi Tavoite, kolmas painos, 2014)
- Eliyahu M. Goldratt, The Haystack Syndrome, 1990
- Wallace J Hopp & Mark L. Spearman, Factory Physics 3rd Edition, 2008
- Antti Piirainen, Vaihtelu, 2014
Tilaa uutiskirje
Liity postituslistalle ja saat ajankohtaista tietoa tehdasfysiikasta ja laatutekniikoista sekä laadun kehittämisestä suoraan sähköpostiisi.
Tämä lomake on suojattu Google reCAPTCHA:lla. Lue tietosuojaseloste ja käyttöehdot.
Liittymällä postituslistalle hyväksyt Quality Knowhow Karjalainen Oy:n tietosuojaselosteen ja Quality Knowhow Karjalainen Oy voi lähettää sinulle ajankohtaisia artikkeleita, videoita sekä tietoa ja tarjouksia kursseista, kirjoista sekä ohjelmistoista.

Tämä lomake on suojattu Google reCAPTCHA:lla. Lue tietosuojaseloste ja käyttöehdot.