Onko Laatu Leania vai Lean Laatua? – Lean Six Sigma

Oletko huomannut, kuinka marketin kassajonossa asiakkaan ”laatuvirhe”, PIN-koodin unohtaminen, tuotteen hinnan puuttuminen joko punnituksen unohtumisesta johtuen tai muusta syystä vaikuttaa kaikkiin henkilöihin? Jonon pituus kasvaa ja harkitset siirtymistä toiseen jonoon. Maksujonosi ei kulje LEANISTI. Syntyy hukkaa.

Sama tapahtuu uudelleen ja uudelleen kaikkialla – palveluketjussa, yrityksissä, prosesseissa, liikenteessä. Kaikkialla, jossa on mahdollista syntyä ”jonoja”. Laatuvirhe, häiriö lisää jonoutumista! Johtuuko tämä todella virheestä vai mistä? Voidaanko tämä mallintaa ja laskea? 

Jonot ovat suurelta osin laaduttomuuksien seurausta, laatukustannuksia. Laatuvirheiden kokonaismäärä on 25-45 %  kaikista kustannuksista. Virhekustannus itsessään ei ole suurin kustannuserä vaan siitä muodostuvat seuraukset. 

Laatuvirhe, romu, on kaikkein pahin Lean -hukka. Se on myös kaikkein kallein. Laatuvirhe vaikuttaa asiakkaaseen, synnyttää reklamaatioita, aiheuttaa voimakkaan jonoutumisen ja ruuhkan, vaatii uudelleen työtä, syntyy romukustannuksia ja materiaalihävikkiä, ympäristöongelmia jne. Laatuvirhe on todellinen hukkien hukka! 

Laatuvirhe ja jonoutuminen

Miten jonoutuminen, ruuhkat ja pitkät läpimenoajat sekä toimitusvirheet voidaan selittää laatuvirheellä?

Tarkastellaan seuraavaa yhden työaseman tilannetta, joka voi olla kassa, kone, prosessivaihe, palvelupiste, tms. Asemaan tulee joka kolmas minuutti asiakas tai työ (nopeus r_a=1/3) ja työaseman nopeus on t₀=1 työ/minuutti (kapasiteetiksi). Asemassa on myös vaihtelua, sigma σ₀.

Mitä tapahtuu, jos syntyy tietty osuus virheitä? Merkitään virheosuutta p:llä (0-1, 0-100%). P osuus töistä epäonnistuu tai on tehtävä osittain tai kokonaan uudestaan (korjattava).

Suomessa koko palveluketjun tai tehtaan p = luku on 0,2 – 0,7 tai 20 – 70 %. Tällöin ei puhuta yhdestä työasemasta vaan koko prosessista ja saannosta. Mittari on RTY= 1-p (Rolled Throughput Yield) eli ensimmäisellä kerralla oikein!

Määritellään tehollinen keskiarvoaika t_e, jonka asema käyttää työasemasta lähtevien töiden (valmiiden) tekemiseen [1]

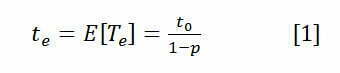
Jos virheitä on p=30 % ja työn nopeus on 1 min/työ, niin ulos meneviin töihin menee keskimäärin aikaa 1/0,7= 1,42 min/työ.

Tämä ei kuitenkaan riitä. Jokainen on meistä marketin kassajonossa manaillut niitä, joilta PIN-koodi tai punnitus on unohtunut. Vaikka emme ole tehneet virhettä, joudumme ”tuon toisen syystä” odottamaan. Kaikki odottavat. Syntyy jono.

Kuinka tämä huomioidaan? Lasketaan, miten virhe vaikuttaa teholliseen vaihteluun, hajontaan σ_e. Kutsutaan myös sigmaksi. Itse asiassa yleensä lasketaan varianssi σ_e2 [2]

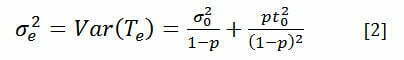
Jotta saadaan vähän parempi vertailuluku suhteessa käytettyyn aikaan, jaetaan vielä varianssi σ_e2 tehollisen ajan neliöllä t_e2, saadaan neliöllinen varianssikerroin SCV (Square Coefficient of Variance) [3]

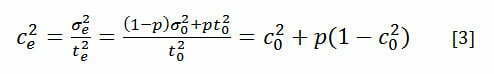
Tarvitsemme vielä yhden uuden suhdeluvun. Kuinka paljon tai tehokkaasti työasemaa käytetään? Tätä kutsutaan yleisesti käyttösuhteeksi u (utilization).

Käyttösuhde on aina pienempi kuin 100 % (<1). Se saadaan jakamalla tuleva työnopeus r_a työaseman tehollisella nopeudella r_e=1/t_e . [4]

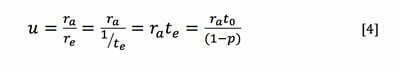
Nyt voidaan tehdä seuraavat välijohtopäätökset:

1. Käyttösuhde u kasvaa epälineaarisesti 1/(1-p) eli virheet (uudelleen tekeminen ja korjaus) syövät prosessiaikaa ja kapasiteettia tehollisen nopeuden pienentyessä. Kun virheiden osuus p (korjausaika) on yhtä suuri kuin prosessiaika kertaa tuleva nopeus eli se määrä, joka oli käyttämätöntä aikaa ilman virheitä, ”prosessi” räjähtää ja tulee epästabiiliksi. Muodostuu ”pullonkaula”. 
   
   Yleensä tässä tapauksessa suomalainen ratkaisu on lisätä kapasiteettia (ja veroja) eikä parantaa prosessia eli vähentää virheitä! Virheitä vähentämällä voidaan alentaa käyttösuhdetta eli ”lisätä” kapasiteettia ilmaiseksi! On tosin osattava virheiden ehkäisytekniikka, Six Sigma. 
   
   Organisaatioissa on hyvin yleinen pyrkimys kasvattaa käyttösuhdetta niin, että työasemat käyvät ”kiireisenä” – näyttää tehokkaalta – mutta valitettavasti jonot kasvavat. Jonojen syyksi nähdään virheellisesti käyttösuhteen huono aste, kun sen sijaan pitäisi lyhentää tehollista aseman aikaa vähentämällä virheitä. Tästä seuraa käyttösuhteen lasku ja mahdollisuus tehdä enemmän. 
   
   Käyttösuhde kyllä ”laskee” kapasiteettia kasvattamalla, mutta se vaatii investointeja ja lisää henkilökuntaa esimerkiksi lisäkassojen käyttöönoton jonoja lyhentämään. Siis tehokkuus laskee! 
   
    
2. Prosessin hajonta kasvaa virheiden osuuden suhteessa. Hajonta, vaihtelu on se, joka itse asiassa aiheuttaa jonot. Jos hajontaa ei ole, ei myöskään ole jonoja! Jonot siis syntyvät ennen käyttösuhteen ”räjähtämistä”, joka tapahtui kun u=1. 

Meillä on kuitenkin vielä vastaamatta, kuinka lasketaan jonon pituus ja miten jonon käy, kun virheiden määrä muuttuu. Kaikkihan me se on koettu, että kun yksi tupeksii, niin muutkin kärsivät. Vaikutus on yleensä paljon enemmän kuin virheen korjaamiseen kuluva aika.

Tähän antaa vastauksen ns. Kingmanin jonoyhtälö eli ns. VUT-yhtälö, joka kertoo yleisen jonotusajan [5]. Tästä yhtälöstä kertoo erinomaisen hyvin kirja ”Tätä on Lean” ^{/3 s.42/}

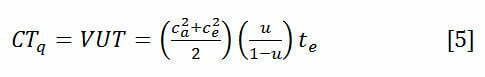
Kingmanin yhtälö on yksi kaikkein tärkeimmistä jono- ja ruuhkateorioiden yhtälöistä, joka yleistää jonoteorian. John Kingman esitti yhtälön 1961. ^/4/ Kingman on nykyajan Newton! Newton -instituutin 3 pääjohtaja.

Yhtälössä ensimmäinen termi kuvaa vaihtelua (Variation) tulevan ja prosessin vaihtelukertoimien neliöinä c_a² ja c_e². Toinen termi käyttösuhdetta U ja viimeinen termi työaseman aikaa T (palveluaika). Yhtälö on voimassa kun u<1.

Kun tähän yhtälöön lisätään vielä prosessin tehollinen aika, saadaan määritettyä, kuinka kauan yhden prosessivaiheen läpi kulkeminen kestää. (CT= VUT + CT). [6]

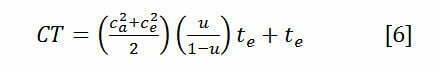
Esimerkissä tutkimme vian tai virheen vaikutusta (virhesuhde p), jossa työ tehdään uudelleen (korjataan tai romutetaan ja tehdään uudelleen), saadaan seuraavilla oletuksilla (tuleva työ r_a=1/3 on kohtuullisen vaihtelevaa c_a2=1, prosessiaika t₀=1 ja työ determinististä c₀=1) seuraava yhtälö koko prosessiajalle CT [7]

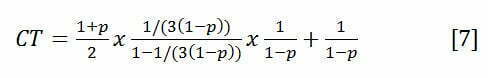
”Sotkuinen” yhtälö, mutta kuvana selväpiirteisempi. Jaksoaika on piirrettynä virheprosentin suhteessa, kun tuleva virtaus on ra=1/4, 1/3 ja 1/2 työ/min aseman kapasiteetista 1 työ/min.

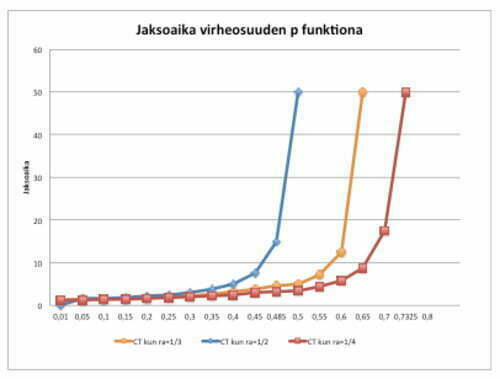
Johtopäätökset jonon muodostumisesta:

1. Virheet ”syövät” kapasiteettia jo paljon ennen kuin käyttösuhde saavuttaa virheiden kuluttaman kapasiteettirajan, läpimenoaika ryöstäytyy kohti ”taivasta”. Tämän näemme usein liikenteessä ruuhka-aikana. Yksikin virhe, ja kaikki seisovat. Samalla tiellä ei-ruuhka sama virhe ei aiheuta oikeastaan mitään ongelmia.  
2. Lähes aina pullonkaulassa tapahtuvat virheet ja uudelleentyö sanelevat yrityksen, palvelun, tuotannon jaksoajan pidentymisen (jonon) ja myös läpimenon nopean heikkenemisen WIP- varastojen täyttyessä. 
3. Tärkeät toisistaan riippuvat tekijät ovat tulevan työn määrä ja vaihtelu c_a, työaseman vaihtelu c_e, käyttösuhde u, johon vaikuttaa tuleva nopeus ra ja aseman kapasiteetti t₀ ja ?₀ ja tehollinen aseman aika t_e 

Jos edellä olevaan yhtälöön [7] sijoittaa r_a=1/3=0,33, p=0 eli NOLLA-virhettä, niin jaksoaika on CT = 1,25 min. Jos koko linjan RTY = 40 %, läpimenoaika CT on pidentynyt 12,5 min.

Perinteisesti virheistä johtuva jonotusaika vie 10-30 kertaa sen ajan, jonka työ parhaimmillaan vaatii. Samalla jono synnyttää keskeneräisen työn, WIP:n. Littlen lain mukaan jono voidaan laskea WIP= TH*CT, jossa TH on läpimeno (TH=1/t_e) tai koko yrityksen läpimeno (kpl/h, kpl/vrk). Aikayksiköt muutettava samaksi.

Yhteenveto

Laatuvirheillä ja niiden korjauksilla ja uudelleen tekemisellä on aivan keskeinen rooli tuotanto- ja palvelutoiminnassa ja Leanissa. Laatuvirheet ovat lähes kaikkien Lean -hukkien takana, juurisyy (korjaus-, ylituotanto-, prosessi-, kuljetus-, varasto-, liike- ja odotushukka).

Lean Six Sigma on yhdistetty virtauksen- ja laadunparannuksen tekniikka, jota johtavat suomalaiset sekä kansainväliset yritykset käyttävät pyrkiessään tehokkaaseen nopean virtauksen ja lyhyen läpimenoajan omaavaan 0-virhe palvelu- ja tuotantoprosesseihin.

Lähteet:

1. www.infineon.com/cms/en/product/applications/automotive/living-automotive-excellence/index.html 
2. W. J. Hopp, Mark L. Spearman: Factory Physics, third edition, 2008 
3. Niklas modig, Pär Åhström: Tätä on Lean – Ratkaisu Tehokkuusparadoksiin, 2013 
4. Zandin, K.B. 2001. Maynard’s Industrial Engineering Handbook 5th edition.