Aikavaihtelu

Tilausten ja tuotteiden välisten aikojen vaihtelun vaikutus yritysten tai organisaatioiden tuottavuuteen on merkittävä. Jos tilaukset tulisivat aina samalla nopeudella, niiden aikaväli ei vaihtele. Jos tuotteet yrityksessä tehtäisiin aina samalla nopeudella (so. liukuhihna), niiden nopeus/aika ei vaihtele. Vaihtelu vaikuttaa resurssien tarpeeseen ja tätä kautta investointitarpeeseen sekä organisaation kykyyn vastata asiakaskysyntään nopeasti ilman korkeaa varastotasoa. Artikkelissa käsitellään luonnollisen, satunnaisten ja ei-satunnaisten sekä laatuvikojen vaikutusta aikaan ja sen vaihteluun.

Aluksi on syytä määritellä muutama perustermi. Organisaatioon on investoitu koneita, laitteita, luotu työpisteitä, tms. tuottamaan tuotteita tai palveluita. Tätä kutsutaan toiminnoksi ja usein prosessiksi, jossa muodostuu asiakkaalle arvoa. Arvolla tarkoitetaan tuotteen tai palvelun ominaispiirrettä (asiaa tai tekijää), kilpailutekijää, josta asiakas on valmis maksamaan enemmän kuin sen tuottaminen maksaa. Arvon tuottaminen, minkä asiakas kokee ja saa, vaatii aina aikaa. Tätä kokonaisaikaa kutsutaan raa’aksi prosessiajaksi (raw process time, T₀) tai ominaispiirteen muodostumisajaksi. Tämä aika on yleensä 0,1-10 % kokonaisajasta, jonka palvelu/tuote on linjassa. Jos vaihtelu poistetaan, työt valmistuvat 10-100 kertaa nopeammin! Palvelun/tuotteen käyttämä kokonaisaika on jaksoaika (kutsutaan joskus läpimenoajaksi). Yksittäisen työvaiheen aikaa kutsutaan teholliseksi ajaksi (t_e).

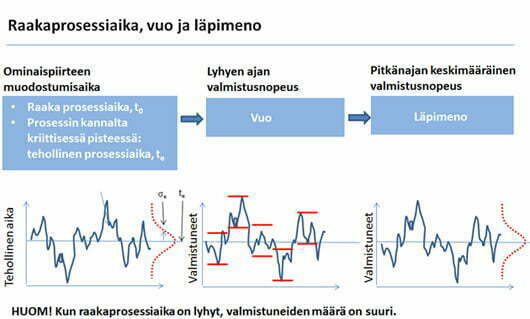
Organisaatiolla on aina rajallisesti resursseja. Tätä rajallista aikaa kutsutaan käytettävissä olevaksi ajaksi (availability time). Jaksoaika vaihtelee aina erilaisista syistä johtuen, joten tuotteita tai palveluja valmistuu eri tarkasteluväleillä eri määrä. Valmistusnopeus vaihtelee. Tätä kutsutaan termillä vuo ja prosessissa tapahtuvaa tuote tai materiaalivirtaa virtaukseksi (flow). Mitä lyhyempi on raakaprosessiaika, sitä enemmän tuotteita valmistuu tietyllä tarkasteluvälillä (katso kuva 1). Yrityksissä halutaan tietää tuotteiden tai palveluiden (arvonmuodostumisen) valmistumisnopeus. Tätä kutsutaan läpimenoksi (throughput), joka tarkoittaa pitkän aikavälin keskimääräistä valmistumisnopeutta.

Ajan vaihtelulähteitä on useita. Vaihtelua tulee tuotantosysteemiin sekä ulkoa että sisältä päin. Tilukset/potilaat tulevat epätasaisesti ja työt liikkuvat epätasaisesti yrityksessä vaiheesta toiseen. Palveluiden tai tuotteiden tuottamisen yhteydessä on tärkeää tunnistaa raakaan prosessiaikaan (kokonaisaikaan) vaikuttavat yleiset vaihtelun lähteet. Toisin sanoen ominaispiirteen muodostumisaika kestää eri ajan ja alkaa vaihdella.

Ajan vaihtelun lähteet:

• ”Luonnollinen” vaihtelu
• Satunnaiset pysähdykset
• Ei-satunnaiset pysähdykset
• Operaattoreiden käytettävyys
• Laatuviat

Yleensä häiriöiden, keskeytysten tms. oletetaan vaikuttavan vain keskimääräiseen ominaispiirteen muodostumisaikaan (0,1-10%) ja unohdetaan vaikutus vaihteluun. Pidentyvä arvon muodostusaika vaikuttaa resurssien käyttöön, mutta unohdetaan tai ei tunneta vaihtelun vaikutusta. Vaihtelu on aina merkittävämpi, koska se kuluttaa yli 90 % tai jopa 99 % koko jaksoajasta.

Vaihtelun vaikutus ominaispiirteen muodostumisaikaan

Tuottaapa organisaatio tuotteita tai palveluita, havaitaan ominaispiirteen muodostumisajassa aina vaihtelua. Tämä vaihtelu on luonnollista. Luonnollinen vaihtelu on tyypillisesti suurempaa manuaalisessa työssä kuin automatisoidussa työssä. Satunnaista vaihtelua on aina.

Riippumatta työstä tai työympäristöstä syntyy joka tapauksessa täysin ennalta tunnistamattomasta syystä johtuvia satunnaisesti ilmentyviä työn pysähdyksiä tai hidastumisia. Nämä tekijät vaikuttavat ominaispiirteen muodostumisaikaan. Nämä voivat olla työntekijän yllättävä sairausloma, konerikko, ”hätäpalaveri”, esimies keskeyttää työn, jne. Pysähdykset voivat olla myös ei-satunnaisista tekijöistä johtuvia pysähdyksiä mutta kysynnän täyttämisen kannalta välttämättömiä. Jälkimmäisistä tekijöistä esimerkkinä voisi olla asetusajat tai työnvaihtoajat, palaverit töiden välissä tms. Käytännössä vaihtelua aiheuttaa mikä tahansa asia joka estää työn tekemisen. Riippumatta tekijästä vaikutus voidaan havaita raa’assa prosessiajassa keskiarvossa (T₀) ja keskihajonnassa (σ₀)

Tyypillisesti vaihtelun suuruutta kuvataan keskihajonnan ja keskiarvon suhteella COV -arvolla (coefficient of variation) c₀= tai neliöllisellä COV-arvolla (SCV) c₀²=. . Luonnollinen vaihtelu c₀ on tyypillisesti alle 0,75. Seuraavana tarkastellaan kuinka satunnainen, ei-satunnainen ja laatuviat vaikuttavat keskiarvoon ja keskihajontaan.

Esimerkki keskeytysten tai työn vaikeutumisen vaikutuksesta keskiarvoon ja keskihajontaan

Ajatellaan, että asiakkaalle palvelun/ tuotteen tuottaminen kestää 1 minuuttia (t₀) ja luonnollinen vaihtelu on keskihajontana 0,333 minuuttia (σ₀). Yksinkertaisuuden vuoksi tässä on vain yksi työasema eli T₀=t₀. COV-arvo on 0,333min/1min = 0,333 ja SCV =0,111. Yhden päivän aikana käytettävissä (A₀) on 420 minuuttia. Ideaalitilassa, jossa ei ole häiriötä toiminnon läpimeno (r₀) on 420 tuotetta per päivä (r₀=A₀/t₀).

Satunnaiset pysähdykset

Toimintoa on tarkasteltu tarkemmin ja yksittäisiä syitä erittelemättä on havaittu että toiminnossa esiintyy satunnaisesti ilmeneviä häiriöitä. Järjestelmästä johtuvista ongelmista tai yllättävistä palavereista johtuen työ keskeytyy keskimäärin 100:n minuutin välein (m_f) ja korjaus kestää keskimäärin 25 minuuttia (m_r). Häiriöiden esiintymisvälin ja keskimääräisen korjausajan avulla voidaan laskea toiminnon käytettävyys (A) ja tehollinen aika, t_e.

Työn pysähdysten vaikutus käytettävyyteen ja ominaispiirteen muodostumisen keskiarvoon on usein tunnistettu ja helposti ymmärrettävissä. Huomataan, että häiriöt aiheuttavat t₀ kasvamisen ja saadaan arvioitua tehollinen aika (t_e) jota voidaan käyttää läpimenon laskemiseen ja resurssisuunnitteluun. Usein kuitenkin jostain syystä jätetään käsittelemättä satunnaisten häiriötekijöiden vaikutus keskihajontaan. Koska kyseessä on ominaispiirteen muodostumisajan pysäyttävä tapahtuma, aika pyrkii kasvamaan eikä laskemaan. Todellisen tilanteen tarkastelussa käyttökelpoinen todennäköisyysjakauma on eksponenttijakauma, jolla kuvataan normaalia toisistaan riippumattomia tapahtumia. Häiriön vaikutuksen vaikutuksesta hajontaan tarvitaan kolme uutta määritelmää: tehollisen ajan varianssi, neliöllinen COV ja korjausajan neliöllinen COV. Hajonnan vaikutus voidaan laskea seuraavasti:

Viimeisimmässä kaavassa ensimmäinen termi on alkuperäistä luonnollista vaihtelua kuvaava tekijä. Kaavan toinen termi kuvaa satunnaisista katkoksista johtuvaa vaihtelua. Kolmas termi kuvaa katkoksen korjauksesta tulevaa vaihtelua. Jos ajatellaan, että itse korjaus ottaisi aina saman verran aikaa, tulee kolmannesta termistä vaikutukseton (c_r^2=0). Tämä tuskin on mahdollista ja sen poistaminen pienentäisi vaihtelua merkittävästi. Esimerkin yksinkertaistamiseksi käytetään esimerkissä arvo c_r^2=1. Tämän jälkeen voidaan soveltaa kaavaa:

Laskelmasta huomataan, että keskiarvo kasvoi 1 minuutista 1,25 minuuttiin ja keskihajonta 0,333 minuutista 1,666 minuuttiin. COV-arvo on 1,333

Ei-satunnaiset pysähdykset

Jatketaan samaa esimerkkiä ei-satunnaisten pysäytysten osalta. Ajatellaan, että tuotevaihtoa tapahtuu keskimäärin kerran joka päivä. Vaihto tapahtuu keskimäärin kahdensadan tuotteet välein (Ns). Vaihto kestää keskimäärin 30 minuuttia (ts) ja vaihtoajan keskivaihtelu on 10 minuuttia (?s).

Tehollinen ominaispiirteen muodostumisaika saadaan laskettua lisäämällä raakaan prosessiaikaan (jos ei huomioida edellä esitettyjä häiriöaikoja) vaihtoaika per erän aikana tuotettu tuote.

Vaikutus keskiarvoon on usein huomioitu tarjouslaskenta ja tuotannonsuunnittelussa. Pysähdysten vaikutus keskihajontaan on jäänyt huomioimatta. Tästä seuraa suuret erot tarjouslaskennan ja toteutuneiden aikojen/kustannusten välillä! Vaihtelun vaikutusta muodostuvaan kokonaisvalmistusaikaan käsitellään artikkelin lopussa. Pysähdysten vaikutus vaihteluun saadaan laskettua seuraavasti:

Samoin kuin satunnainen vaihtelu, ei-satunnainen tekijä lisää luonnollisesti keskimääräistä aikaa, mutta merkittävämpi vaikutus on vaihteluun. Ce= 2,143/1,15= 1,863.

Laatutekijä

Listan viimeinen muttei vähäisin on laatu. Laatu tarkoittaa kuinka onnistutaan tuottamaan sitä mitä on suunniteltu. Laatu sekoitetaan yleensä ominaisuuteen (tavoitearvo), kun kysymyksessä on vaihtelun hallinnasta suhteessa tavoitteeseen.

Ajatellaan, että esimerkkitapauksessa toiminnossa täytyy onnistua kymmenestä eri tehtävästä, josta muodostuu tuote tai palvelu. Yksittäinen tapahtuma onnistuu yhdeksänkymmentäviisi kertaa sadasta. Ensimmäisellä kerralla oikein onnistuminen (RTY, rolled throughput yield) voidaan laskea tästä helposti (0,9510=0,599). Epäonnistuminen, joka johtaa tuotteen tai palvelun korjaukseen tai työn uudelleen suorittamiseen tapahtuu keskimäärin siis vähintään yhdessä tehtävässä noin neljänkymmen prosentin todennäköisyydellä 

Ominaispiirteenmuodostumisajan keskihajonta voidaan laskea seuraavasti:

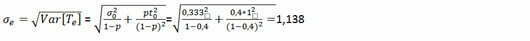
COV-arvo on σ_e/t_e = 0,497/1,67=0,683

Tarkemmin tästä Eero E. Karjalaisen artikkelissa ”Onko laatu Leania vai Lean laatua” 2014.

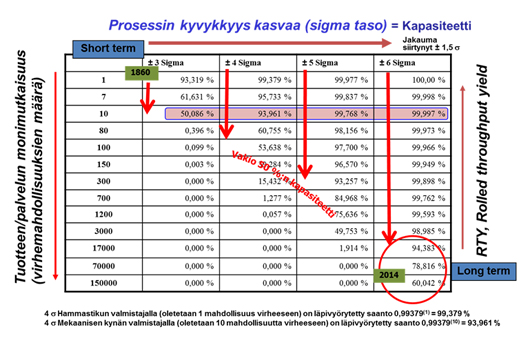
Syksyllä 2008 eräässä yrityksessä aloitettiin tuottavuuden parantaminen. Kun toimintaa tutkittiin havaittiin RTY:n olevan kolmekymmentä prosenttia. Parannustoimenpiteet RTY:n ja tämän myötä myös muut toimenpiteet mahdollistivat merkittävän tuotannon tehostumisen. Oleellista on alkaa laadusta, koska laadulla (uudelleen tekemisellä) on merkittävin vaikutus tuottavuuteen. Ei siis pelkästään romu- ja reklamaatiokustannuksiin, vaan aikaan. Näin myös Toyotalla. Laatu on nro 1. Keskeiset tunnusluvut ovat seuraavassa taulukossa.

Motorolalla (länsimaissa) havaittiin laadun merkitys tuottavuuteen ja asiakastarpeen täyttämiseen seitsemänkymmentäluvun lopussa. Tohtori Mikel J. Harry ja J. Ronald Lawson käsittelevät laatuongelmaa Motorola University Pressin julkaisussa 1992. Laatuongelman ratkaisemiseksi kehitettiin menetelmä. Menetelmä tunnetaan Lean Six Sigmana.

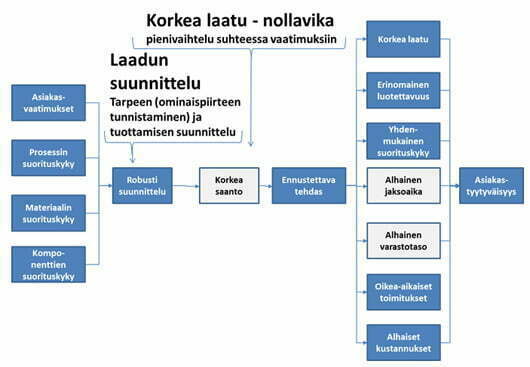
Johtopäätökset

Kuten edellisistä esimerkeistä huomataan, suhteellinen muutos hajontaan on suurempi kuin keskiarvoon (taulukko 1). Usein ajatellaan virheellisesti, että ongelmat vaikuttavat vain keskiarvoon, vaikka tuottavuuden kannalta tärkeämpi tekijä on aika- ja ominaisuusvaihtelu. Esimerkeissä käsitellään vain yksitäistä työpistettä. Käytännössä organisaatiossa on tapahtumaketjuja (prosesseja, toimitusketjuja, työasemia, soluja jne.), joissa aika- ja tuotevaihtelun kasvaminen vaikuttaa vaiheiden väliseen riippuvuuteen. Mitä suurempi on vaihtelu, sitä enemmän keskinäisvaikutukset kuluttavat resursseja.

Taulukko 1. Yhteenveto vaihtelua aiheuttavien tekijöiden vaikutuksesta keskiarvoihin ja keskihajontoihin.

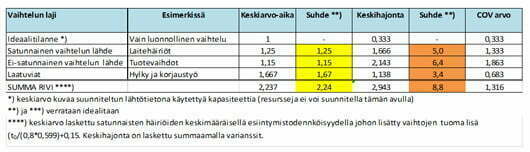
Taulukkoon 1 on koottu esimerkkien luvut. Taulukosta ja esimerkeistä ei voi tehdä yleistystä mikä vaihtelun lähde on merkittävin, koska jos lähtötiedot muuttuvat, myös vaihtelulähteiden painotukset muuttuvat.

Organisaatioissa vaihtelua vastaan varaudutaan käyttäen varastoja, aikaa ja kapasiteettia. Kingmanin yhtälö sitoo yhteen vaihtelun, resurssien käyttöasteen (kysynnän ja todellisen läpimenon) sekä tehollisen ajan ja työpisteen eteen muodostuvan jonotusajan. Yhtälöstä voidaan havaita, että jaksoaika kasvaa voimakkaasti tehollisen ajan – COV-arvon – kasvaessa (kaavassa Ce) ja resurssien käyttöasteen u pysyessä vakiona. Yrityksessä tämä havaitaan pitkinä jonoina, isoina toimitiloina, pitkinä toimitusaikoina, laajoina varastoina jne. Kaikki työskentelevät kiireisenä, mutta virtaus on alhainen ja työt ruuhkautuvat. Resurssit kuluvat vaihtelun kompensoimiseen

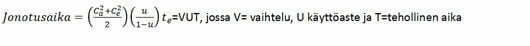
Kuvaan 5 on laskettu edellisen esimerkin avulla kolme skenaariota, joiden avulla kuvataan vaihtelun merkitystä. Lähdetään kasvattamaan toimintoon kohdistuvaa kysyntää 20 kpl per päivä kohti kapasiteettia 420 kpl per päivä. Tämä vaikuttaa käyttöasteeseen. Toiminnon käyttöaste lasketaan tehollinen aika (te) jaettuna keskimääräisellä kysyntävälillä (ta), eli te:ta=u Esimerkissä kysynnän vaihtelu ca=2.

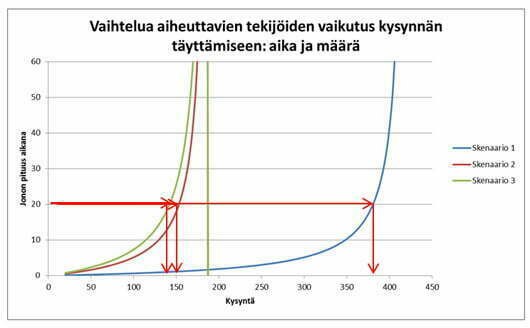
Kuvasta 5 havaitaan, että kysynnän täyttäminen käy mahdottomaksi kun kysyntä nousee yli 130-140 kpl per päivä. Käytännössä investoituun kapasiteettiin nähden resurssien käyttöaste on alle 25 %. Todellisuudessa kaikki ovat kiireisiä, koska he käyttävät aikaa aikavaihtelua aiheuttavien tekijöiden kompensoimiseen. Helposti syntyy illuusio, että resurssien käyttöaste on korkea, vaikka todellisuudessa aika hukkuu virheitten korjaamiseen, joka kuluttaa käyttöastetta. Jos toiminnan tehokkuuden arvioimista tehdään alkutilanteeseen verrattuna (t0,s0), toimenpide johtaa väistämättä epästabiiliin tilaan.

Kuormituksen kasvaessa noin 180 kpl per päivä tuotantosysteemi ajautuu epästabiiliin tilaan. Varastotasot alkavat kasvaa räjähdysmäisesti ja jaksoajat kasvavat. Paniikkinappula pohjaan, alkaa ylireagoiminen, joka vain lisää vaihtelua (jos toimenpide ei kohdistu kapasiteetin kasvattamiseen = kustannusten kasvattamiseen). Ainoaksi keinoksi hallita vaihtelua aiheuttavia tekijöitä jää laskea käyttöastetta. Organisaatioissa resurssien käyttöasteen laskeminen toteutetaan investoimalla ”ylikapasiteettiin”, vaihtelulta suojaaviin varastoihin tai pidennetään toimitusaikoja. Kaikki toimenpiteet laskevat kilpailukykyä. Autoteollisuudessa ja muualla massateollisuudessa aikavaihtelun hallinta on numero yksi.

Lähteet:

• Deming, W. E. 1982. The Out of the Crisis. Massachusetts Institute of Technology Central for Advanced Engineering StudyCambridge.
• Forrester, J.W. 1971. Principles of Systems. Productivity Press. USA.
• Harry, M. J. & Lawson, J.R. 1992. Six Sigma Producibility Analysis and Process Characterization. Motorola University
• Hopp, W. J. & Spearman, M. L. 2008. Factory Physics third edition. McGraw-Hill Irwin.
• Zandin, K.B. 2001. Maynard’s Industrial Engineering Handbook 5th edition. McGraw-Hill.
• Wheeler, D. J. 2010. Reducing Production Costs. SPC Press, Knoxville, Tennessee.